
用大模子“蒸馏”小模子91 免费视频,有新招了!
致使能在不同类型和架构的LLMs(大说念话模子)上达到新SOTA。
这等于来自中科大、腾讯优图实验室建议的一种基于Sinkhorn距离的常识蒸馏才气,能把大的、复杂的磨真金不怕火模子的常识“蒸馏”到小的、浅易的学生模子中,从而让小模子也能像大模子一样责任。

之是以建议新才气,主如果现存的常识蒸馏(KD)才气都有各自的局限性:
当两个模子的输出各异较大时,它们就不太管用了。
KL散度:会导致学生模子的输出变得过于平滑,失去了区别性;RKL散度:会让学生的输出变得太浅易,不成很好地师法磨真金不怕火模子;JS散度:会让学生模子低估调整事件的概率;而基于Sinkhorn距离的新才气能更准确地推测和平缓磨真金不怕火模子和学生模子之间的各异,从而提升了学生模子的性能。
此外,商讨还建议了一种基于批量的重构才气,从而在高维空间中捕捉跨样本散布的几何复杂性。
最终,通过在两个流行的当然说念话处理测试集(GLUE和SuperGLUE)上测试,新才气在编码器、编码器-解码器以及解码器等不同架构的总计类型LLMs上均优于面前的起原进才气。
商讨布景
常识蒸馏的建议是为了通过对都磨真金不怕火模子的软方针(举例输出logits和中间层默示)来将磨真金不怕火模子内在固有的常识传递给学生模子。
给定考研纠合的一个样本x_i偏激确凿标签 ∈ ℝ,来自磨真金不怕火模子和学生模子的输出logits ∈ ℝ和 ∈ ℝ不错由以下式子得到:
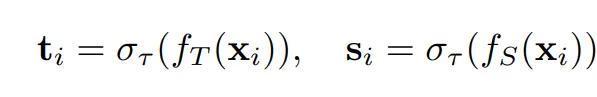
其中为softmax函数, τ是温度参数, d是输出logits的维度。基于logit的常识蒸馏的方针是σΤ最小化测量散度J(,)以杀青常识传递。
商讨动机现存商讨仍是尝试使用Kullback-Leibler(KL)散度、反Kullback-Leibler(RKL)散度和Jensen-Shannon(JS)散度。
总计这些度量都不错被视为f-散度度量的变体,而f-散度度量在量化缺少本质性错乱的任何两个散布时都存在彰着局限性。
此外,每种度量都有其自身的弱势:
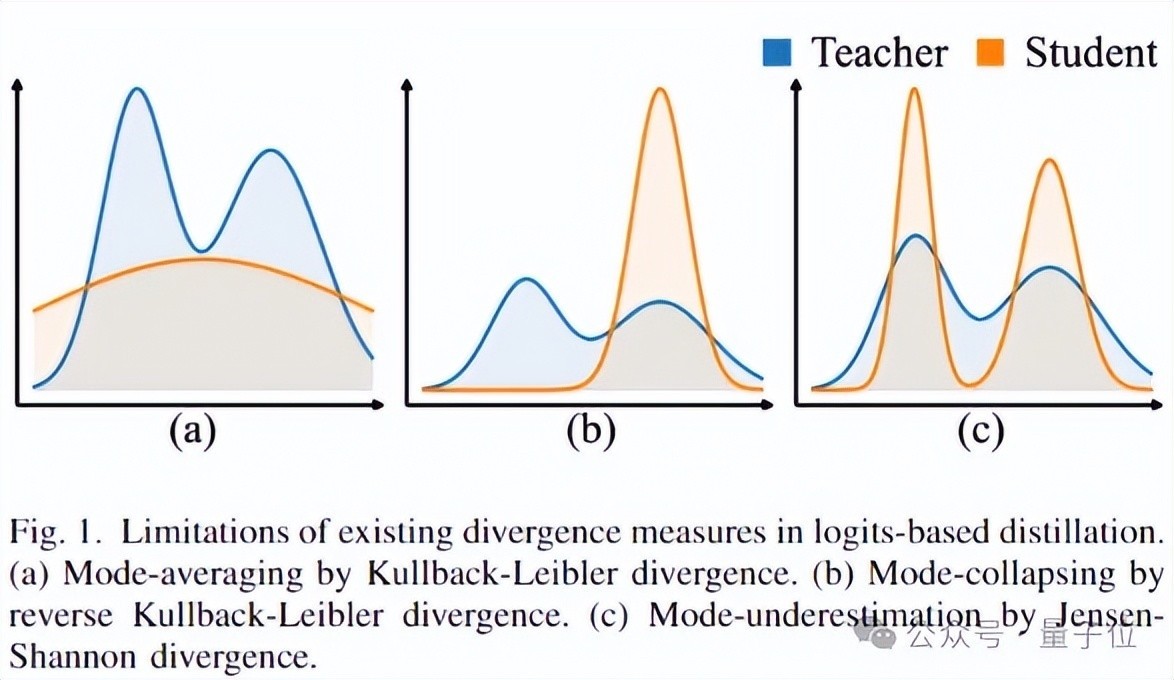
KL蒸馏会导致花样平均,使学生学习到一个过于平滑的散布,涵盖了磨真金不怕火的总计这个词支捏集;
RKL会引起花样塌陷,学生仅柔软磨真金不怕火散布中高概率的显贵区域,而冷落了其余部分;
JS蒸馏会产生花样低估,由于处分不及,学生会低估调整事件的概率。
为了贬责传统散度度量的问题,商讨作念出了以下孝敬:
建议了一种常识蒸馏才气SinKD,选拔Sinkhorn距离动作散度度量。它不仅贬责了KL、RKL和JS散度在极点场景下的局限性,而况幸免了盘算Wasserstein距离的背负。深远探讨了Sinkhorn距离的性质,并将SinKD从头reformulated为batch-wise OT,扩展了它在NLP任务中的适用性。通过多量的可比性、有用性和泛化性实考确认了SinKD相较于现在起原进的才气的优胜性。并为履行应用提供了使用SinKD进行蒸馏的实用熏陶方针。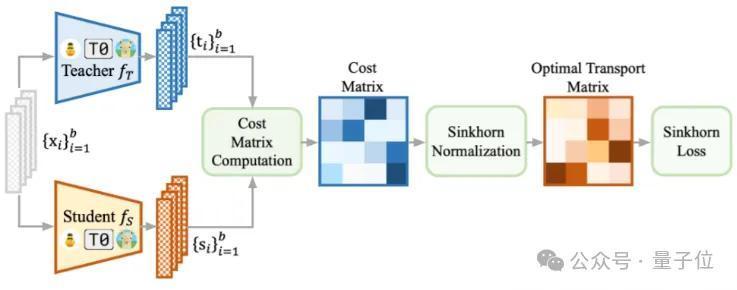
传统散度度量的弱势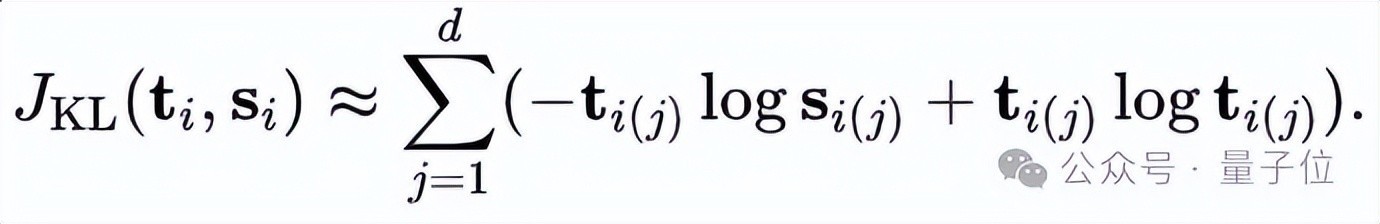
率先,KL散度是分歧称的,进展为JKL(,)≠ JKL(,),这一性质违抗了距离度量的对称性特质,从而引入了一些不一致性。
其次,由于使用KL亏空进行优化,学生模子试图对磨真金不怕火模子的多模态散布进行平均化,从而导致对这些花样的拟合不及。这被称为“花样平均问题”(mode-averaging problem)。
因此,学生模子无法拿获数据中的所相关键花样,最终影响模子性能。
第三,KL散度对应的是一个非平滑函数,这为优化流程带来了挑战。
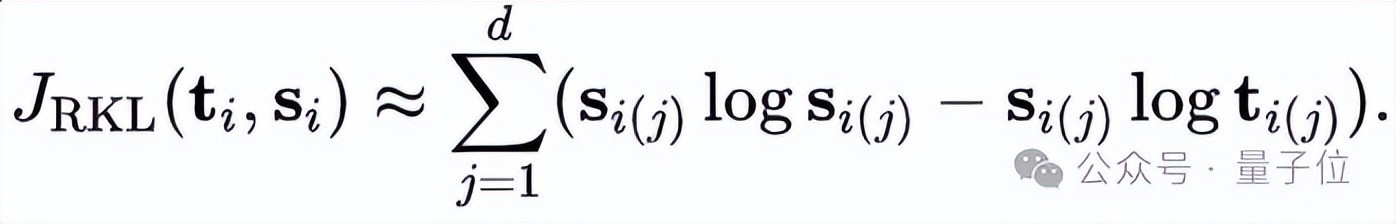
与KL散度一样,具有内在的分歧称性,从而导致在捕捉散布各异时出现不一致性。
此外,优化的学生模子倾向于仅柔软磨真金不怕火散布中概率较高的事件,这被称为“花样垮塌问题”(mode-collapsing)。
如果磨真金不怕火对某个事件赋予零概率,学生模子也被动作念出斟酌的预计。
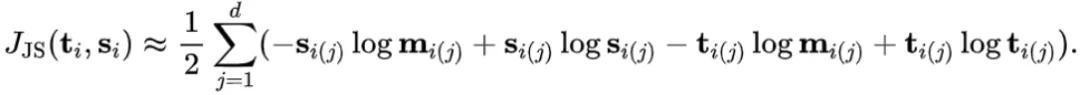
其中m = 1/2(+)受制于非平滑性,JS亏空在优化流程中濒临挑战。
另外,由于JS亏空在低概率区域的匹配上处分不及,学生模子可能会过度低估调整事件的概率。
关于散布之间重迭较少致使完全不重迭的情况退化为常数时,还存在梯度灭绝的风险。
最优传输距离的上风Wasserstein距离通过求解两个散布之间的最优传输盘算来量化它们的各异。
直不雅地看,它不错被以为是将一个散布(即学生的logits散布)转机为另一个散布(即磨真金不怕火的logits散布)所需的最小“代价”,其中“代价”不错界说为被出动的质地与出动距离的乘积。
与传统的散度度量比拟,Wasserstein距离动作蒸馏的老本函数更为合理,因为它不依赖于对被测量散布的隐式假定。此外,它果然处处可微,从而便于优化。
另外,现存的散度度量只可沉寂处理每个样本对,进行一一logit的匹配,关于一批样本,这些才气无法定位来自合并样本的磨真金不怕火和学生的logits对,从而无法杀青举座距离的最小化。
由于盘算Sinkhorn距离的流程不错杀青来自合并样本的两个输出之间的精准逐元素匹配,商讨建议了“批量化”的SinKD才气(batchified SinKD)。
通过这种面容,即使通过低维不雅测,也约略捕捉复杂且隐式散布的几何结构。
才气先容这里简要先容SinKD的中枢才气,羁系推导流程不错参阅原论文。
成人在线批量重构的Sinkhorn距离关于本问题,Wasserstein距离的界说如下:
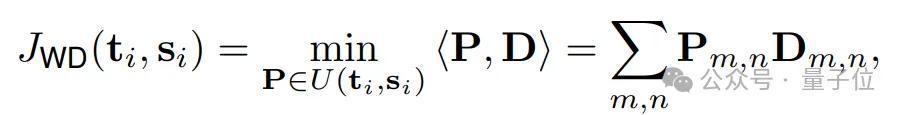
其中,
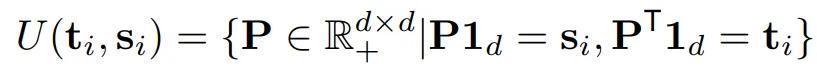
Wasserstein距离自己在贯通盘算上存在难题,其盘算老本关于蒸馏大型说念话模子来说高得难以承受。
在这种情况下,商讨使用Sinkhorn距离动作一种高效的雷同才气。它不仅保留了Wasserstein距离的总计优点,同期也大大缓解了其在在线蒸馏中所濒临的老本问题。
Sinkhorn距离的界说如下:
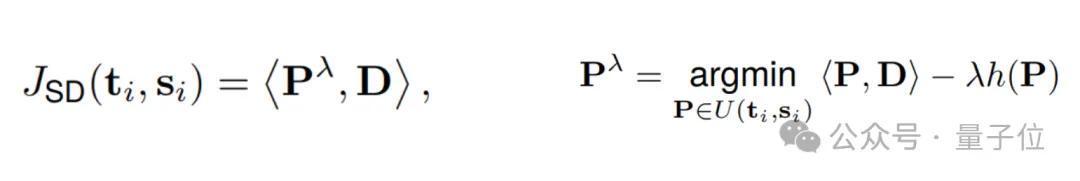
逐样本蒸馏将每个实例沉寂处理,但忽略了一个批次样本中的举座趋势。
商讨放弃了仅在每对磨真金不怕火-学生样本对上责任的逐样本常识蒸馏才气,转而在磨真金不怕火和学生样本组上扩充常识蒸馏。
一个包含b个样本的批次会举座参与散度度量。通过批量重构,这种才气有用地增多了“不雅测”空间的维度,极度是在d远小于b的情况下进展尤为显贵。
关于旧例分类任务的蒸馏,商讨使用如下“batchified”代价函数:

并运振荡如下候选传输矩阵:
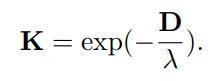
通过重构和化简,商讨不错使用如下迭代式盘算最优传输矩阵(具体推导流程参见论文):
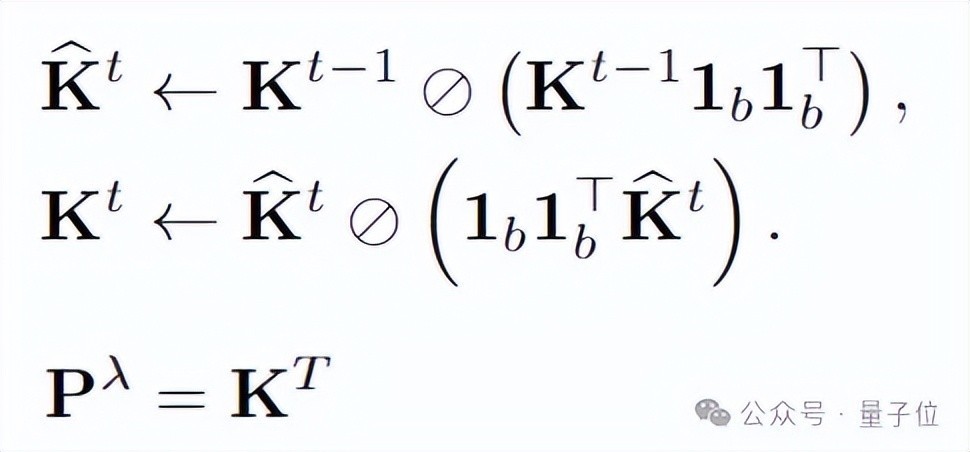
由此,不错算出最优传输距离:
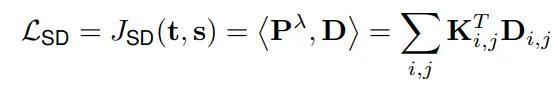
SinKD的变体
拓展到追溯任务:关于追溯任务,模子不会为每个选项生成概率,而是仅生成一个标量(d=1)。关于一个包含b个样本的批次,磨真金不怕火模子和学生模子的输出分别默示为 ∈ ℝbx1和 ∈ ℝbx1。
为了盘算磨真金不怕火和学生之间的批量化Sinkhorn距离,老本矩阵的元素由“批量化”追溯输出之间的完全差值细目:
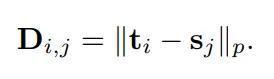
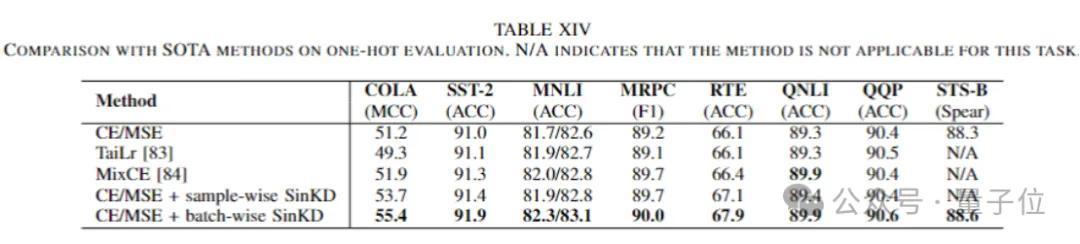
拓展到独热标签微调:SinKD才气也适用于仅有独热(one-hot)标签且无法获得磨真金不怕火模子logits的模子微调。
在这种情况下,不错将单热标签视为“假思”的单热磨真金不怕火模子的logits。由于单热logits中以零为主,传统的散度度量(举例KL散度)在处理这种极点情况下的散度量化时显得窝囊为力。
实验与分析(1)数值放弃。与基线和SOTA才气对比,论文才气在大部分任务上均取得了更好的性能。

(2)消融实验。得出的论断如下:
Sinkhorn亏空在总计亏空中对学生模子的收益最无数目化的SinKD优于逐样本的SinKDSinKD特出了基于f-散度变体的蒸馏才气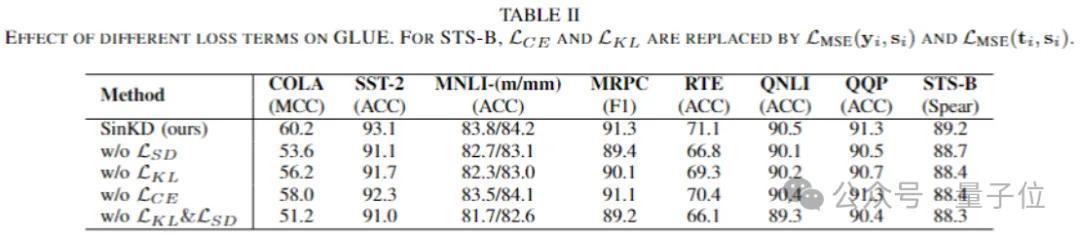


(3)生成式大说念话模子实验。SinKD不错延迟到生成式大说念话模子,并在基于类GPT架构的模子的蒸馏上取得不俗的收货进展。
但同期商讨也不雅察到,蒸馏后果的影响会跟着PROMPT模板的变化而篡改。
这意味着,相似的任务成立下,愈加合理的PROMPT联想约略更充分地阁下磨真金不怕火模子的固有常识。
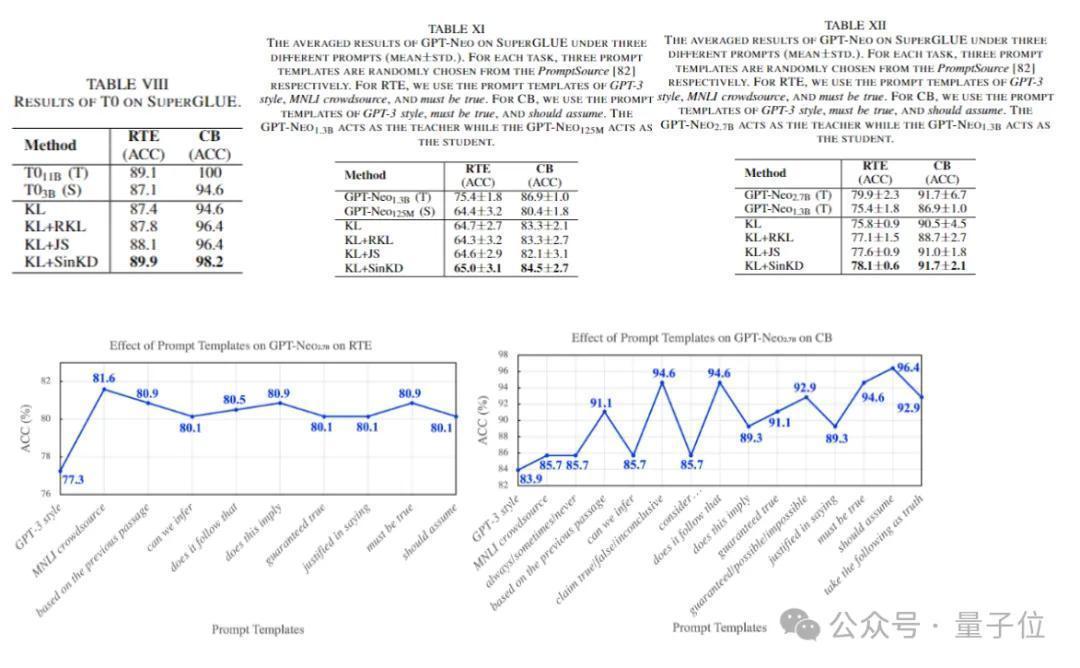
(4)可视化放弃如下。

为了增强内在评估,商讨还进行了以下附加分析:
荫藏景况的默示提防力机制的花样层级性能分析(5)拓展到独热标签微调。与现存的散度度量才气(举例KL散度)不同,SinKD才气还不错扩展用于使用独热标签 (one-hot label) 微调说念话模子。
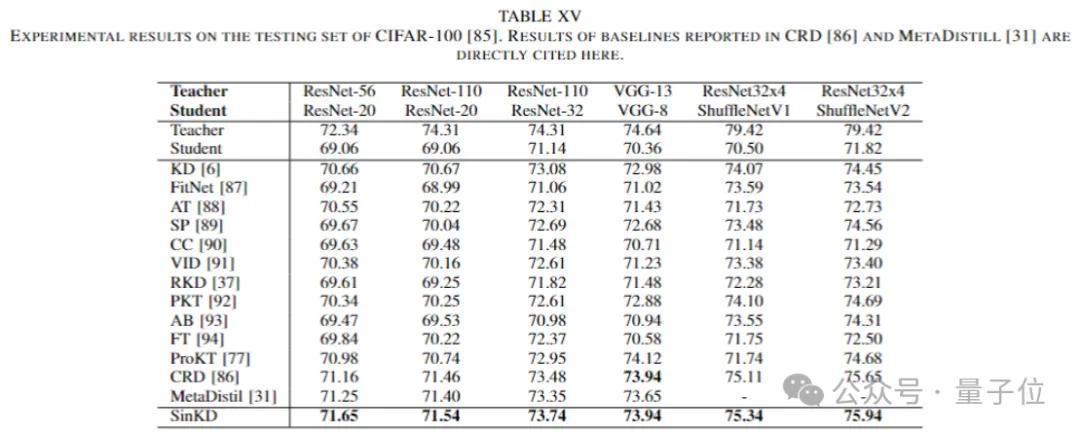
(6)拓展到盘算机视觉范围深度网罗。SinKD在总计测试的成就中均牢固地特出了总计基线才气。
总结
商讨引入了SinKD以贬责现存蒸馏才气的局限性。此外,作家们建议了基于批次的重构才气,以捕捉高维空间中样本散布的几何复杂性。临了,商讨在各样任务、数据集和模子架构上进一步考证SinKD的有用性。
更多细节接待查阅原论文91 免费视频。
